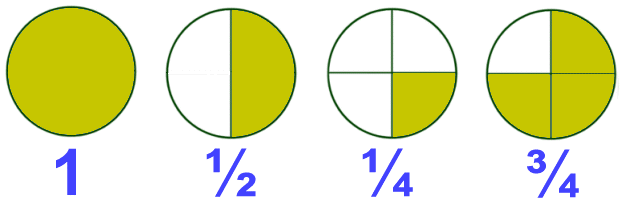
Basic Principles of Fractions

Published February 16, 2023 (updated: March 14, 2023).

Medication administration would be a lot easier if the medication was just packaged in the exact amount that is needed. Unfortunately, this is not the case. Sometimes, medics need to only give half of the packaged amount. Sometimes, medics need to administer more than one package of a medication to a patient that is extremely large. The basis for understanding how much of a medication to give comes from the ability to understand and employ fractions.

Fractions

Fraction- mathematical representation of parts to a whole. The bottom number is the denominator, which is the total number of parts. The top number is the numerator, or the number of parts being represented.

Fractions are representing a part of a whole. A fraction can also be viewed as a division problem where the numerator (number on top) is divided by the denominator (number on bottom).

1 (numerator)
__________
4 (denominator)In medicine, we usually do not administer an entire amount of medication; we only administer a fraction of the whole amount. It is very easy to look at the medications you deliver in terms of giving a half of this or a third of that. Fractions allow us to easily visualize the amount we are to give the patient.

Addition

The first rule of addition is that you can only add like quantities, for example, various quantities of quarters. Unlike quantities, such as adding thirds to quarters, must first be converted to like quantities as described below.

Adding like quantities

Imagine you have a pocket containing two quarters, and another pocket containing three quarters; in total, you have five quarters. Since four quarters is equivalent to one (dollar), this can be represented as follows:

$\textstyle{\frac24+\frac34=\frac54 = 1\frac14}$ .

Adding unlike quantities

To add fractions containing unlike quantities (eg. quarters and thirds), it is necessary to convert all amounts to like quantities. It’s easy to work out the type of fraction that we need to convert to, simply by multiplying together the two denominators (bottom number) of each fraction.
Suppose we are adding quarters to thirds, then we will convert both types of fraction to $\textstyle{\frac14 \times \frac13=\frac1{12}}$
Consider adding the following two quantities:
$\textstyle{\frac34+\frac23}$ .
First we convert $\textstyle{\frac34}$ into twelfths by multiplying both the numerator and denominator by three: $\textstyle{\frac34 \times \frac33 = \frac9{12}}$ . Note that $\textstyle{\frac33}$ is equivalent to $\textstyle{1}$ , which shows that $\textstyle{\frac34}$ is equivalent to the resulting $\textstyle{\frac9{12}}$
Secondly, we convert $\textstyle{\frac23}$ into twelfths by multiplying both the numerator and denominator by four: $\textstyle{\frac23 \times \frac44 = \frac8{12}}$ . Note that $\textstyle{\frac44}$ is equivalent to $\textstyle{1}$ , which shows that $\textstyle{\frac23}$ is equivalent to the resulting $\textstyle{\frac8{12}}$

Now we can see that:
$\textstyle{\frac34+\frac23}$ is equivalent to:
$\textstyle{\frac9{12}+\frac8{12}} = \frac{17}{12} = 1\frac{5}{12}$ .

This always works, but sometimes there is a smaller denominator that will also work (a least common denominator). For example, to add 3⁄4 + 5⁄12, we can use the denominator 48, but we could also use the smaller denominator 12, which is the least common multiple of 4 and 12.

$\textstyle{\frac34+\frac{5}{12}=\frac{9}{12}+\frac{5}{12}=\frac{14}{12}=\frac76}$ .

Subtraction

The process for subtracting fractions is, in essence, the same as that of adding them: find a common denominator, and change each fraction to an equivalent fraction with the chosen common denominator. The resulting fraction will have that denominator, and its numerator will be the result of subtracting the numerators of the original fractions. For instance,
$\textstyle{\frac23-\frac12=\frac46-\frac36=\frac16}$ .

Multiplication by whole numbers

If you have a quarter of the cake and you multiply the amount by three, then you end up with three quarters. We can write this numerically as follows:

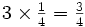
\textstyle{3 \times {1 \over 4} = {3 \over 4}}

As another example, suppose that five people work for three hours out of a seven hour day (ie. for three sevenths of the work day). In total, they will have worked for 15 hours (5 x 3 hours each), or 15 sevenths of a day. Since 7 sevenths of a day is a whole day and 14 sevenths is two days, then in total, they will have worked for 2 days and a seventh of a day. Numerically:

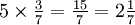
\textstyle{5 \times {3 \over 7} = {15 \over 7} = 2{1 \over 7}}

Multiplication by fractions

Considering the cake example above, if you have a quarter of the cake and you multiply the amount by a third, then you end up with a twelfth of the cake. In other words, a third of a quarter (or a third times a quarter) is a twelfth. Why? Because we are splitting each quarter into three pieces, and four quarters times three makes 12 parts (or twelfths). We can write this numerically as follows:

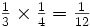
\textstyle{{1 \over 3} \times {1 \over 4} = {1 \over 12}}

As another example, suppose that five people do an equal amount work that totals three hours out of a seven hour day. Each person will have done a fifth of the work, so they will have worked for a fifth of three sevenths of a day. Numerically:
$\textstyle{{1 \over 5} \times {3 \over 7} = {3 \over 35}}$

You may have noticed that when we multiply fractions, we simply multiply the two numerators (the top numbers) and multiply the two denominators (the bottom numbers). For example:

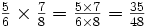
\textstyle{{5 \over 6} \times {7 \over 8} = {5 \times 7 \over 6 \times 8} = {35 \over 48}}

Multiplication by mixed numbers

When multiplying mixed numbers, it’s best to convert the whole part of the mixed number into a fraction. For example:

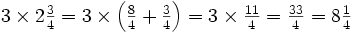
\textstyle{3 \times 2{3 \over 4} = 3 \times \left ({{8 \over 4} + {3 \over 4}} \right ) = 3 \times {11 \over 4} = {33 \over 4} = 8{1 \over 4}}

In other words, $\textstyle{2{3 \over 4}}$ is the same as $\textstyle{({8 \over 4} + {3 \over 4})}$ , making 11 quarters in total (because 2 cakes, each split into quarters makes 8 quarters total) and 33 quarters is $\textstyle{8{1 \over 4}}$ , since 8 cakes, each made of quarters, is 32 quarters in total.

Division

To divide by a fraction, simply multiply by the reciprocal of that fraction.

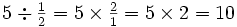
\textstyle{5 \div {1 \over 2} = 5 \times {2 \over 1} = 5 \times 2 = 10}

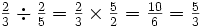
\textstyle{{2 \over 3} \div {2 \over 5} = {2 \over 3} \times {5 \over 2} = {10 \over 6} = {5 \over 3}}

To understand why this works, consider the following:

Question, does

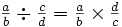
\textstyle{\frac a b \div \frac c d = \frac a b \times \frac d c}

Given/Accepted

I. Any number divided by itself is one (e.g. $\textstyle{\frac d d = \frac 1 1}$ )

II. When a number is multiplied by one it does not change (e.g. $\textstyle{\frac a b \times \frac 1 1 = \frac a b \times \frac d d = \frac a b}$ )

III. If two fractions have common denominators, then the numerators may be divided to find the quotient (e.g.

$\textstyle{\frac {ad}{bd} \div \frac {bc}{bd} = ad \div bc}$ )